※記事に記載された所属、職名、学年、企業情報などは取材時のものです
波の動き、電波が伝わる様子、葉っぱが木から落ちる様子……。これらの身近な現象を「すべて数式で表せる」と言うと、あなたは驚くだろうか。
物理現象を表す代表的な数式として知られる、偏微分方程式。その秘密を解き明かそうとしているのが、千葉大学大学院理学研究院の前田昌也准教授だ。
前田准教授は、特定の偏微分方程式を解析すると出てくる「ソリトン」という「不思議な波」の挙動を研究している。この研究成果は数学界で語られてきた「とある問題」を部分的に解決するものとして高く評価され、2020年に文部科学大臣表彰、2022年には千葉大学先進学術賞を受けた。たゆまぬ探究を続ける前田准教授に、研究や教育にかける思いを伺った。

数学の厳密な視点から物理現象をひもときたい

――先生は、なぜ数学の研究をはじめられたのですか?
子どもの頃から自然や宇宙に興味があったので、京都大学理学部に入学しました。当初は物理を専攻したいと考えていましたが、その後自分は数学の厳密な考え方が好きなことに気づき、3年生になるときに数学系に進みました。
しかし、物理への興味自体は続いていました。そこで4年生では、数学の立場から物理を扱う「数理物理」を学べる研究室を選択。その研究室を運営していた堤誉志雄教授が偏微分方程式の大家だったので、私も自然と偏微分方程式の研究に取り組むようになりました。
――そもそも、偏微分方程式とは何なのでしょう?
偏微分方程式は、かんたんに言えば「物理現象のルールを数式で表したもの」です。水面に現れる波の動き、ボールが落ちる様子、風の吹き方……。これら身の回りの物理現象は、すべて偏微分方程式で表現できます。
では、偏微分方程式というルールによって実際に波はどう動き、ボールは何秒後に地面に当たるのか。その具体的な挙動を知るには、偏微分方程式を解いてその「解」を得る必要があります。しかし、実は偏微分方程式の中には我々のよく知っている多項式や三角関数、指数関数などで解を表示できないという意味で解けないもの、つまり「解の表示」が得られないものが存在します。このような意味で解けない偏微分方程式の挙動を研究するのは、数学界の一大テーマです。
私は、一般には解けない偏微分方程式の一種として考えられている「非線形シュレディンガー方程式」と、その代表的な解である「ソリトン」について研究しています。
「ソリトン分解予想」の部分的な証明に成功

――ソリトンとは何ですか?
ソリトンとは、「孤立して存在する不思議な波」です。普通の波は移動するにつれて形が崩れるものですが、ソリトンは同じ速度と形を保ったまま長い距離を伝わります。非線形シュレディンガー方程式を含むあるクラスの偏微分方程式でよく見られる解です。
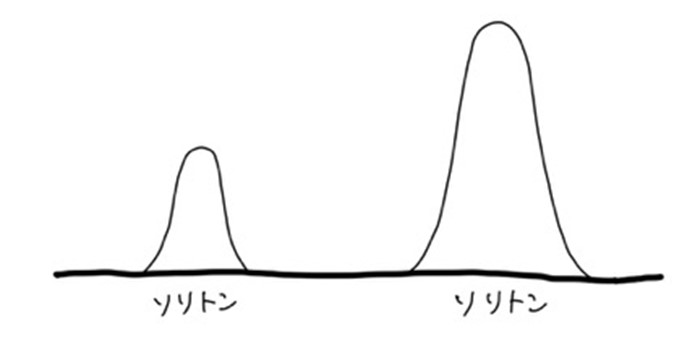
このように一見変わった挙動を示すソリトンですが、実はさまざまな物理現象の中で実際に観測されています。例えば日常スケールでは、浅い水面の波。ミクロのスケールでは、光ファイバー内の光の伝搬。マクロのスケールでは、低気圧の動きや大気中の突風、そして宇宙のブラックホールまで。あらゆるところにソリトンは隠れているのです。
――このソリトンが、「非線形シュレディンガー方程式」の「一般的な解の挙動」だと予想されていると
そうです。これを「ソリトン分解予想」といいます。この分野に関わる研究者にとってはこの予想を証明することがひとつの大きな目標であり、私も長年取り組んでいます。
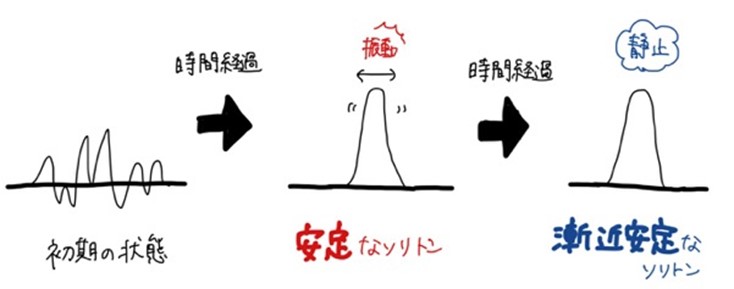
ソリトン分解予想を証明するには、ソリトンが「解」として現れ、かつその形状が変化しないことを示す必要があります。ここで重要なのが、ソリトンの「安定性」「漸近安定性」という2つの概念です。
「安定性」とは、ソリトン解の形が大きくは崩れないという性質です。「漸近安定性」は安定性の先にある概念で、安定なソリトンの振動が抜けてその形状が変化しなくなってゆく性質を指します。ソリトン分解予想を解決するには、すべての解がソリトンに近づき、なおかつソリトン解が「漸近安定」になるまでの過程をすべて証明する必要があるのです。
――なるほど。先生は、これらをすべて証明されているのですか?
最終的なゴールはもちろんそこなのですが、現代数学ではかなり難しいというのが現状です。私が引退する25年後までに証明できたら驚き、というレベルの話ですね。そこで、私は安定なソリトンの振動が抜けて漸近安定になる過程にフォーカスして研究しています。
現時点で、ある種の振動パターンを持つソリトンの漸近安定性を証明することに成功しています。この証明は、比較的多様なソリトンに適用できる手法という点で高く評価いただき、2020年には文部科学大臣表彰をいただきました。今後は、より多様な振動パターンを持つソリトンを扱えるように研究を続ける予定です。
ソリトンの安定性や漸近安定性の研究は、光ファイバー内の光を安定させて伝送距離を長くするといった応用技術にもつながる可能性があります。私自身はソリトンの数学的な解析自体におもしろさを見いだしていますが、私の研究成果を誰かが応用して社会実装してくれるとうれしいですね。
大自然が与えてくれる「豊かな構造の方程式」を研究したい

――研究テーマを決める上で意識されていることは?
「豊かな数学的構造を持つと期待される方程式」を研究したいと思っています。例えば、自然現象を表す方程式ですね。流体の動きを表すナビエ-ストークス方程式などは200年近く研究されていますが、今でもすばらしい数学的発見が次々と生まれ、海洋の循環、大気の動きなどを説明するための重要なツールとして使われています。大自然は、本当に研究しがいのあるおもしろいモデルを与えてくれるのです。
しかし中には、物理の分野では自然現象を表すよい方程式だと思われていても、数学的には「解」が発散したり不安定になったりして、うまく自然現象を表せないものもあります。そういった方程式も興味深いですね。
――先生は元々物理に興味があったというお話でしたが、研究テーマを決める際にも物理とのつながりを意識されているのですね
そうですね。あとは、多くの人が参画している分野は基本的に避けるようにしています。私は競争が好きではないので……。あまり人が研究していないトピックを選び、じっくり腰を据えて細かい部分まで研究するのが私のスタイルです。
興味ある問題をじっくりと考えるのが、数学の醍醐味
――世の中には「数学が苦手だな」と感じている人も多いと思います。そういった方々が数学のおもしろさを知るには、どうすればいいのでしょうか?
数学が苦手になる原因のひとつは、子ども時代の経験にあるのではないかと思います。子どもの頃はテストや受験に合格するために、「与えられた問題を短い時間で正確に解く」ことが求められますよね。これでは、数学が嫌いになるのも無理はないでしょう。
しかし、実は数学の本質は全く別のところにあります。数学とは「自分の興味ある問題を、1日や2日、あるいは1年以上かけてのんびりと考える」学問なのです。これを広く伝えられれば、子ども時代の呪縛から解放されて数学を好きになってくれる人が少しは増えるのではないでしょうか。
――最後に、先生の研究に興味を持った学生へのメッセージをお願いします
基本的には、好きなことや知りたいことを優先して研究してほしいと思います。自身の興味関心に向き合って、長く取り組める研究テーマを見つけてほしいですね。
とはいえ、数学の場合は各分野を表面的に眺めるだけでは全く理解できないのが普通なので、はじめから自分で研究テーマを見つけるのは難しいでしょう。最初は指導教員の指示に従って本や論文を読み、指定された分野の研究を進めながら、自分の興味ある分野を見つけていけばいいと思います。
最終的には、指導教員に対して「あなたの研究はつまらない」「こっちの方がおもしろいよ」とまで言えるようになってくれるとうれしいですね。共に数学を楽しみ、その奥深い世界を探求できる。そんな方をお待ちしています。

インタビュー / 執筆

太田 真琴 / Makoto OTA
大阪大学理学研究科(修士)を卒業後、組込みSEとして6年間勤務。
その後、特許翻訳を学んでフリーランス翻訳者として独立し、2020年からは技術調査やライティングも手がけるように。
得意な分野は化学、バイオ、IT、製造業、技術系スタートアップ記事。
「この人の魅力はどこか」「この人が本当に言いたいことは何か」を問いながらインタビューし、対象読者に合わせた粒度の記事を書くよう意識しています。











