「微分方程式」を「図形」に変換する！？～数式と幾何をつなぎ、新たな世界のマッピングに挑む 千葉大学 大学院理学研究院 准教授 廣惠 一希[ Kazuki HIROE ]

『私は微分方程式の「路線図」を描いているんです』。そう生き生きと話すのは、理学研究院の廣惠一希准教授だ。

廣惠准教授は「微分方程式」を「図形」に変換することで、数式のままでは見えなかった微分方程式同士の関連性を描こうとしている。数式の世界にいる「微分方程式」と、幾何の世界にいる「図形」。これらの全く異なる概念を結びつけると、一体何が起こるのだろうか。

「数学の面白さは人間臭さにある」と楽しそうに語る廣惠准教授に、現在の研究内容や今後の展望を伺った。

微分方程式を「回転」させて図形に変形する

―最初に、先生のご研究について教えてください。

私は、さまざまな微分方程式*を図形として表現することで、微分方程式同士の関連性を調べる研究をしています。微分方程式に限らず数学的対象の多くは目には見えませんよね。私は、微分方程式を点と線からなる図形（グラフ）として表現することで複雑性をそぎ落とし、微分方程式の本質を分かりやすく可視化しようとしています。

*正確には、微分方程式の一種である「代数的な線形微分方程式」を扱う。この微分方程式は係数部分が多項式で表され、数式処理や図形処理などのさまざまな処理を統合的に適用しやすいことが知られている。

これは言わば、「自分のポケットから手探りで目的の小物を取り出す」ようなものです。私たちは、ポケットの中をわざわざ覗かなくても、手の感触だけで必要な小物を間違えることなく取り出せますよね。それは、ポケットの中に何が入っているかを全て知っており（たとえば「カギ」と「財布」）、かつそれらの形（ギザギザ、四角いなど）を認識しているからです。私は、これに近いことを微分方程式に対して行っています。微分方程式は実際に見ることができないので、それらを図形として「解釈」し、それらの図形を「分類」することで、微分方程式を新たな側面から見える化しようとしているのです。

－どのようにして微分方程式を図形に変換するのでしょうか？

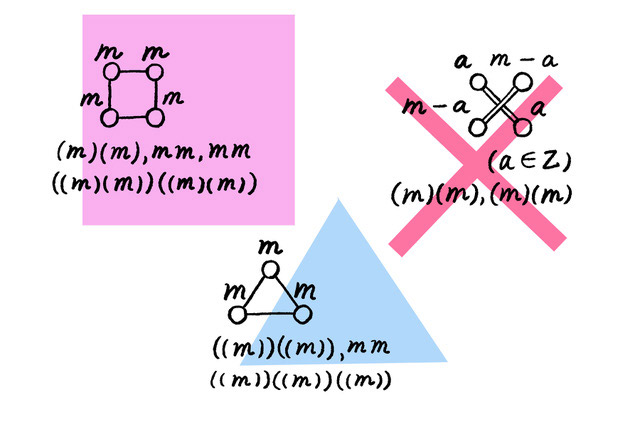
私の研究では、「回転対称性」と呼ばれる性質を使います。これは「図形をある角度だけ回転させたときに、その図形が元と同じ形になる性質」です。たとえば、正三角形は120度回転させると元と同じ形になるので「120度の回転対称性」をもち、正方形は90度回転させると元と同じ形になるので「90度の回転対称性」をもちます。逆に考えると、ある図形の形が正確に分からなくても、その回転対称性を調べれば形状をある程度予測できます。

回転対称性は本来図形がもつ性質ですが、微分方程式も図形のような対称性を持つことに興味を覚えました。微分方程式に対して「まるで図形を回転させるような操作」をして、微分方程式がもつ「回転対称性」を調べることで、目には見えない微分方程式の「形」を特定するのです。もちろん、微分方程式を物理的に回転させるのは無理なので、あくまでも「回転に対応する数式変換」を施すという意味です。

私はこの回転対称性を活用して、微分方程式を図形に変換する方法や、逆に図形から元の微分方程式に戻す方法などを研究しています。

モジュライ空間を「駅」に見立てた微分方程式の「路線図」を描き、最もかんたんな微分方程式を見つけ出す

－微分方程式を図形で表すと、どんなよいことがあるのですか？

微分方程式を図形で表現することで、同じ図形に変換される微分方程式の集まり（「モジュライ空間」と呼ばれる）を定義できます。さらに、あるモジュライ空間に対応する図形が別のモジュライ空間の図形に変換できる場合、それらのモジュライ空間同士は関連性があるとみなせます。つまり、モジュライ空間を「駅」、関連性を示す線を「線路」ととらえた、以下のような「微分方程式の路線図」が描けるのです。

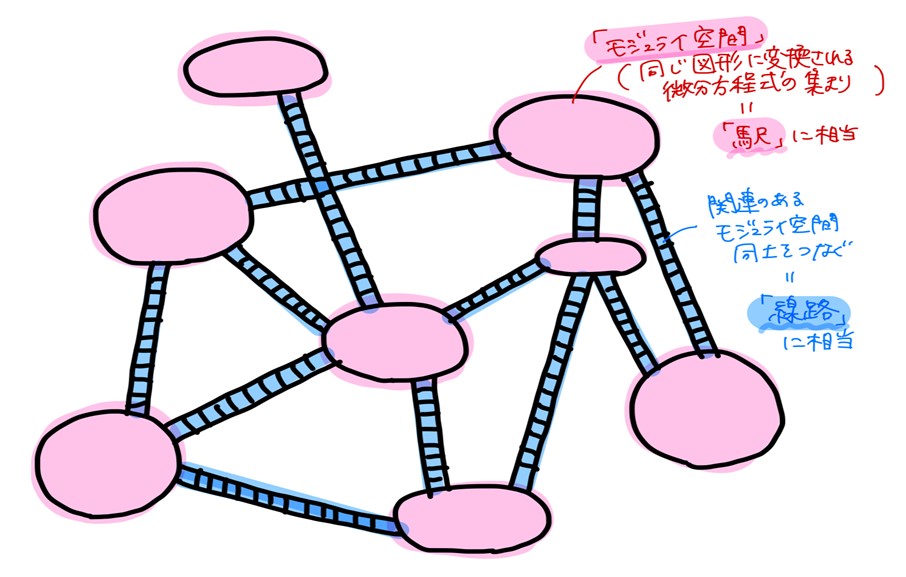
この路線図において、線路でつながっているモジュライ空間は全て同じ性質をもちます。つまり、線路をたどって一番かんたんな微分方程式を含むモジュライ空間を見つけ、その中の微分方程式を解けば、線路でつながっている全モジュライ空間の微分方程式を解いたことになるのです。解きにくい微分方程式を解く方法を見つけるのに、この路線図が大いに役立つということですね。

微分方程式自体は無数に存在するため、数式のままでは路線図が書けません。しかし、図形への変換を通して同じ性質の微分方程式をグループ化することで、駅（モジュライ空間）を定義できるようになったのです。図形を使うことで、数式からは分からなかった微分方程式同士の関連性を明らかにできた点がこの研究のキモですね。

－なるほど、この「路線図」が先生の成果なのですね。

そうですね。しかし、現在の方法ではまだ全ての微分方程式を図形に変換できるわけではありません。より幅広いクラスの微分方程式を図形化できるようになれば、路線図中に登場する駅（モジュライ空間）や線路の数が増えるため、今よりもさらにかんたんな微分方程式を見つけられるはずです。

現在はさらに、モジュライ空間同士を関連付けるための新たな手法も開発中です。今後も、路線図をより緻密に描くための研究を続けていきます。

－先生の研究は、どのような分野に応用される可能性がありますか？

微分方程式のモジュライ空間は素粒子物理学に出てくる空間と似ているらしいので、素粒子物理学とは何らかの形で関われるのではと期待しています。将来的には共同研究ができたら楽しそうですね。

人と人とのコミュニケーションが数学の醍醐味

－先生は元々理工学部に在籍していたと伺いました。なぜ大学院から数学科に進んだのですか？

「自分の使っている数学をきちんと理解したい」と思ったからです。私は理工学部の材料工学科出身で、学部時代は原子構造や分子構造について学びました。しかし、それらの理論で使われている数学が非常に難しく、ほとんど理解できなかったんです。学部生として授業を受けるうち、理解できていない数学を道具として使うことに徐々に違和感を覚え、「自分は数学の理論そのものを学べる環境の方が向いているのでは」と考えるようになりました。悩んだ末、思い切って大学院では数学専攻の受験にチャレンジすることにしました。

－数学のどのような点が面白いと感じますか？

数学の世界には化学や物理のような実験がなく、基本的には紙とペンだけで研究を進めます。理論をつくり、その誤りを見つけられるのは、今のところ人間の頭脳だけと言えるでしょう。このような環境で重要なのが、「人と人とのコミュニケーション」です。

数学はある種競技のような側面があり、スピードとかパワーというか、個人の能力差が目に見えてしまうことがあります。私は特に、中途で数学専攻に入ったこともあって周りとの力の差は歴然で、圧倒されてしまうことも多かったのですが、幸い人に恵まれました。先生や同級生、他大学の研究者など、多くの人たちとコミュニケーションをとり、アイデアやヒントを積極的に交換しながら研究を進めるなど、人と人との繋がりの中に楽しさを見つけて今に至っています。全然面識がなかった数学者と、雑談から数学の面白い話に発展することもよくあるんですよ。こういった「人間臭さ」が、数学の大きな魅力だと思います。

自らのバックグラウンドを生かし、多くの分野と交流したい

－今後はどのように研究を進める予定ですか？

せっかく他分野から数学専攻に入ったので、数学の世界だけに閉じこもらず、さまざまな分野と積極的に交流していきたいと考えています。私の出身である材料分野をはじめ、多くの分野と共同研究ができるとうれしいですね。数学の世界でつくってきたコミュニケーションの輪を、他分野にもどんどん広げていきたいです。

－最後に、学生や若手研究者へのメッセージをお願いします。

「自分の専門はこれだ！」と決めつけず、広い視点をもってほしいですね。高校から大学、大学院と進む中で専門を決めないといけない場面もあるかと思いますが、世界にはあなたの知らない面白い研究がまだまだたくさんあります。専門にこだわりすぎて行動範囲を狭めるのは、本当にもったいないことです。ぜひ、若いうちにいろいろなことに挑戦してほしいと思います。

多くの人とコミュニケーションをとりながら、この広い数学の世界を大いに楽しんでください。

● ●　Off Topic　● ●